于赫夫
认识这个世界,理解这个世界,与这个世界交谈,这大概是人类永恒的追逐,不朽的浪漫。如果上面的所谓“世界”指的是物质和现实空间,那么我们的追求方式就是物理的;如果“世界”指的是逻辑和抽象空间,那么我们追求的方式就是数学的。这两种视角都无穷尽地迷人;而如果能将这二者统一,或许这个世界最本质的面纱才会第一次被稍稍揭开。
大约一百六十年前,用惊鸿一剑稍稍吹动这面纱的人,是黎曼(Riemann)。
彼时,人们认识数字的方式,已经超越单纯的数字计算,开始将数字本身作为研究对象。“数”的存在不依托于现实世界,是纯抽象的,对它的研究特别有利于人们推进对数学本质的认识。而研究一个东西,人们首先想到的就是找到构成它的基本单元。就像物理学为了找到最小的最不可分的那种物质,从公元前4世纪古希腊德谟克里特提出“原子”,到现在的高能物理实验用“深度非弹性散射”考察原子内部的夸克胶子结构,付出了无数心血。那么“数”这个东西,构成它的不可再分割的基本单元是什么呢?
人们发现,最好用的“数”的单元也许是质数,因为质数不能再被(1以外的)其他数字整除,且所有整数都可以写成质数的加减乘除——质数俨然是数字王国的砖块。但问题在于,这砖太飘忽跳脱,你看,从“2,3,5”,到“29,31,37”,再到“401,409,419”,规律何在——这哪里是砖块,简直是四处冒头的地鼠。数学家们头大如斗,这可不是小麻烦。数学江湖一时间风波大动,为了捕捉质数的规律而惊动了各路高手,欧拉(Euler)、高斯(Gauss)、勒让德(Legendre)等大佬依次上阵,最终祭出大阵“质数定理”,将质数的出现规律堪堪约束在一个范围。而此后又该如何,阵脚牢不牢靠,大佬们仍一筹莫展。正在此时,黎曼遥遥一指,一把飞剑将质数牢牢锁住,质数定理这个大阵就此活了,以质数为基石的数论王国迅速走向繁荣。黎曼一生只对质数出手一次,便定了乾坤。
故事详细讲来是这样的。
在距今大约两百六十年前,欧拉为了解决一些数学问题(巴塞尔问题和证明欧几里得定理)而考察了一种实数函数,此后人们对这个函数的计算也局限在实数范围。事情就此尘封,转眼间数学江湖开始了对质数的围剿,一众高手用各自的方法,将质数的出现规律约束在一个差不多相同大小的范围。由于人们的思路往往是在实数战场解决实数问题,用函数思想抓住函数规律(用一个函数来描述质数出现的规律),因而最终都走到了相似的终点,遇到同样巨大的困难。而黎曼则站在截然不同的高度看待这个问题。他首先超脱实数概念的束缚,尝试使用更宽阔的视角,同时又超越函数的束缚,以“函数的函数”,也就是泛函的思想找寻规律。当他想到尘封中的那个被欧拉考察过的实数函数,黎曼知道自己可以落子了。
那年黎曼32岁,刚刚荣选为德国柏林科学院院士,任职于哥廷根大学作教授,意气风发。这位英俊腼腆的数学天才“春风得意,看尽长安”的方式,是发表了一篇论文《论小于已知数的质数的个数》("On the Number of Primes Less Than a Given Magnitude")。这篇论文只有八页,堪称小巧,然而里面宏大的思想却震动了那个时代,轰鸣至今。
在论文中,黎曼将欧拉考察过的那个实数函数扩展为复数函数,著名的复数Zeta函数就此出现了
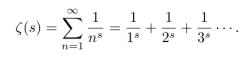
其中s是复数自变量。复数由两部分组成,一部分的平方大于等于零,叫做实部,一部分的平方小于零,叫做虚部。把一个实数函数用“解析延拓”(也就是保持函数的解析性质不变的同时,扩大函数的定义域)的方式扩展为一个复数函数,在当今看来是常规技术,但在一两百年前用这招解决实数问题确有些惊世骇俗。在图象上表示复数,需要一个实数轴表示实部,和一个虚数轴表示虚部,因而可以说复数构成一个平面(也就是复平面),这相比实数构成一条线(实轴)有很大区别和便利,允许人们使用复分析中丰富的武器,对问题进行“降维打击”。黎曼在论文中进一步把Zeta函数写成“其他函数的函数”(也就是泛函),从而厘清了Zeta函数的零点(也就是让函数取值为0时的自变量的值)的分类。零点有两类,一类是与三角函数有关的零点,规则地分布在实轴上,叫做“平凡”零点(平凡的意思就是说,这些零点比较容易全部找到,完全掌握,且对质数分布这个问题的影响没那么深刻);另一类零点就是规律较复杂的,分布在复平面上的零点。至此,黎曼对质数下手了:他(和后人不断地)论证了,人类预言的质数出现规律和真实情况之间的误差,完全掌控在他的Zeta函数零点的手中。尤其让人感兴趣的就是非平凡零点对上面的误差的影响,对于这类零点,人们很容易证明它们分布在复数平面的一个带状区域内。而黎曼就此给出了更精确的预言,也就是著名的黎曼猜想:
“很可能所有非平凡零点都位于实部为1/2的一条线上”。
像他以往的很多论断,黎曼没有给出证明,因而让人遗憾和沉醉。在很多现代数学家看来,黎曼猜想是最难以攻克也最值得人沉迷的数学难题之一。黎曼猜想的巨大价值体现在很多方面,例如在密码学领域,该猜想的准确证明可以颠覆当今的一大类加密方式。而从认识世界的角度去看,黎曼猜想可以作为一个桥梁,神妙地让人们可以用“谱”的视角同时看待物质世界和抽象数学。
我们看一束光,既可以把它看作一大堆连续的电磁波动,也可以提取出这个波动包含哪些频率,从而用光谱去分析它。这样的思想可以推广开来,人们考察很多“连续”的问题,都能将其分解为一系列分立单元。这个思想在数学和物理学中都有着重要地位,例如数学上的傅里叶变换,以及物理上的谱分析。
当人们的研究视角转向更加本质的问题,也就是当数学开始研究数字本身,而物理学开始研究场和空间本身的时候,需要把规律连续的整数分解为跳脱的质数,以及把场和连续的四维时空分解为分立的、量子化的时空的“谱”。黎曼猜想和Zeta函数可以很好地解决质数出现频率的问题,换言之可以很好地将数字分解为一系列“质数的谱”;而人们惊奇地发现,在分解场和连续时空时,黎曼的那把飞剑依然隐隐在我们身边。
在量子场理论,或者说将微观物质的场和能级“分解”为分立的态的时候,算符和希尔伯特空间是必备的工具,精细结构常数是用量子理论分析原子能级的必然产物,而这一切都被人们发现与Zeta函数有着联系。希尔伯特(Hilbert)和波利亚(Polya)曾建议一种证明黎曼猜想的方法,那就是认为Zeta函数的非平凡零点联系着一类算符的本征值,这既是数学证明的常用方法,也这恰好是量子力学寻找本征态和本征值的基本方法。换言之,等价地将Zeta函数与量子态联系起来的思想由来已久。这一思想被后人不断发展,最终发展出引入特定的量子化条件,将Zeta函数的零点的虚部(也就是和实数无关的那部分)量子化的方案,这与量子力学的框架几乎完全重合。
在时空或者说引力量子化方面,Zeta函数同样大显身手。数学家柯纳(Connes)为了证明黎曼猜想,将时空及其上的场用Zeta函数表示出来,之后一发不可收拾,发明了一整套使用Zeta函数将整个物理空间(包括四维时空和物质场的内部自由度空间)用“谱”表示出来的方案。这是一套全新的量子化方案,提供了深刻的理解世界的视角,也让菲尔兹奖获得者柯纳顺手成为了一名理论物理学家。
回顾开头,我们说黎曼提出Zeta函数和黎曼猜想的目的只是为了“抓住”数字的不可再分割的单元,但如今他的工作却兜兜转转,抓到了客观物理量子化的门径。由于黎曼Zeta函数的零点是完全脱离物质世界的抽象概念,因而黎曼Zeta函数与前沿理论物理的结合,哪怕只是美丽的偶然,已经足以让数学逻辑照亮客观物理的深处。而如果黎曼猜想被最终证明,那么众多学者构造的纯数学逻辑和物理规律的联系将被彻底夯实,最终很可能出现一条畅通的路径,让人类可以在寻找这世界的基本单元的问题上,从纯粹的数学逻辑迷宫豁然走入物质的大千世界。因而只要稍稍碰触黎曼猜想的证明,便足以让数学界鼎沸,让物理学工作者或惊或喜或恐惑地颤栗。
就在最近,阿蒂亚(Atiyah)爵士公布了自己成功证明黎曼猜想的消息,他论证的切入点是量子物理的重要成果,精细结构常数。阿蒂亚爵士和柯纳同为菲尔茨奖得主,乃当今数学江湖两大巨擘。整个数理学界都在翘首等待着这项证明细节的公布,仿佛等待远处的狂风吹来,盼能再次御动那大约一百六十年前的飞剑。
黎曼那惊鸿的一剑却仍仿佛无知无觉,静静伫立在数理的莽原上,如一座界碑。而莽原上的拓荒者则攀过它,跋向远方。


























留言